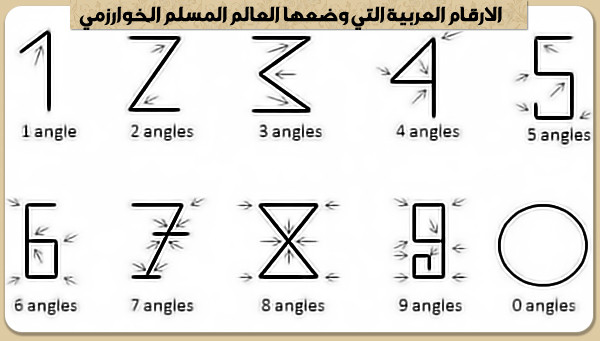
موسوعة هل تعلم: معلومات عن الأرقام (الأعداد)
الرقم والأرقام ليست عدداً أو أعداداً، وإنما هي أشكال تكتب بها رموز الأعداد، والأرقام محدودة وعددها عشرة وهي 9-8-7-6-5-4-3-2-1- 0، لكن الأعداد لا ينتهي عدها – أي ليس لها آخر – فلا يوجد عدد نقول عنه أكبرالأعداد قاطبة.
فرمز العدد سبعة يتكون من رقم واحد هو 7 . ورمز العدد سبعة وعشرين يتكون من رقمين هما الرقم 7، والرقم 2.
وعليه فالرقم يشير إلى عدد من الأعداد، ومن المعتقد أن الأرقام العربية والأعداد الرومانية ترجع هيئتها إلى استعمال أصابع اليد. والعدد يشير إلى تعداد بضعة أشياء أو مجموعها، أو إلى مواقعها في قائمة مرتبة.
وتقوم الرياضيات الحديثة والتي نعيش جميعنا في ظلها الآن على مفهوم العدد، والعدد الكامل بصورة خاصة .
وهكذا صارت لدينا الأعداد العقلانية التي تكتب على شكل كسور، وهناك الأعداد اللاعقلانية، والأعداد المركبة، والأعداد المفرطة في تعقدها، والأعداد الكاترينيونية …. إلخ.
وعلى هذا النحو يتحول الحساب إلى ميدان، وأوسع منه بكثير ميدان الجبر الذي يدرس كل الأعداد والعلاقات العامة فيما بينها .
عناصر المحتوي
هل تعلم أن:
| حاصل ضرب 1089 × 9 هو 9801. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| أول من ابتدع النظام العشري في العد هم المصريون القدماء. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| أول من اكتشف الدائرة منذ عام 500 ق.م هم المصريون القدماء. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| توصل خبراء الرياضيات إلى أن هناك 177,147 طريقة لربط رابطة العنق. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| أول من أعطي قيمة صحيحة للنسبة التقريبية هو غياث الدين الكاشي. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| أول من وضع نظرية الزمر هو الفرنسي إيفاريست جالوا (1811 – 1832 م). | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| حاصل ضرب 111,111,111 × 111,111,111 هو 12,345,678,987,654,321 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| أول من بيّن طريقة إيجاد الجذر التكعيبي هو أبو الحسن علي بن أحمد النسوي. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| أول من توصل لقانون حساب مساحة الدائرة = ط نق2 هو العالم المصري أحمس. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| أوّل من وضع أسس علم الجبر هو العالم المسلم أبو الحسن محمد بن موسى الخوارزمي. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| أول من اخترع النسب المثلثة هو أبو جابر البتاني محمد بن سنان الحراني، ولد ببتان 850 م. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
2520 هو أصغر رقم يقبل القسمة على الأرقام من 1 إلى 10 ويكون الناتج رقم صحيح دون كسور:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| أول من أضاف العدد صفر إلى مجموعة الأعداد 1، 2، 3، ….. لتكون الأعداد الطبيعية هو الخوارزمي. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ناتج مضاعفة الرقم 21978 لأربعة أمثالة (21978 × 4) هو نفس الرقم بترتيب معكوس أي 87912. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ابتكر نيوتن علم حساب التفاضل والتكامل خلال فترة من الزمن تعادل متوسط الوقت الذي يستغرقه طالب للإلمام به. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| أوّل من حوّل الكسور العاديّة إلى كسور عشريّة في علم الحساب هو غياث الدين جمشيد الكاشي، قبل عام 840 هجرية /1436 م. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| أول من اخترع الآلة الحاسبة هو الفرنسي بليز باسكال عام 1642 م لإجراء عمليات الضرب والقسمة بواسطة عجلات تحمل الأرقام. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| أول من أدخل علامة الكسر العشري هو جمشيد بن محمود بن مسعود، الملقب بغياث الدين، ولد بمدينة كاشان بإيران، ولذلك يعرف بالكاشي. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| كشفت الدراسات الحديثة أن الأشخاص الذين اعتادوا مضغ اللبان يحققون نتائج أفضل في امتحانات الرياضيات أكثر ممن يمتنعون عن مضغه. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| قام الصينيون باختراع أوّل معداد يدوي في التاريخ، واستعانوا به على إجراء العمليات الحسابية، وذلك في العام 1000 قبل الميلاد وسموه (الأبوكس). | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| أوّل من استعمل الرموز أو المجاهيل في علم الرياضيات هم العرب المسلمون، فاستعملوا (س) للمجهول الأول، و (ص) للثاني، و )ج) للمعادلات للجذر .. وهكذا. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| أوّل رسالة عن علم الرياضيات طبعت في أوروبا كانت مأخوذة من جداول العالم المسلم أبي عبد الله البتاني، وقد طبعت هذه الرسالة الأولى عام 1493م في اليونان. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| اعتمدت بلاد بابل النظام الستيني في الرياضيات بديلًا عن النظام العشري، وهذا هو السبب في أن الساعة صار بها 60 دقيقة ومجموع قياس زوايا الدائرة هو 360 درجة. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| أول من توصل لحساب طول السنة الشمسية هو أبو الحسن ثابت بن قرة، ولد عام 836 م في حران، وهو وثني من عبدة النجوم، وقد حدد السنة الشمسية بـ 360 يوما و 6 ساعات و 9 دقائق و 10 ثواني. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| أوّل من استعمل الأسس السالبة هو العالم المسلم السموأل المغربي، وهو عالم اشتهر باختصاصه في علم الحساب، وهو أوّل من استعمل الأسس السالبة في الرياضيات، وتوفي هذا العالم الفذّ في بغداد عام 1175م. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| شهدت الحضارة إلانساينية زخمًا من التطور العلمي والمعرفي بداية من القرن العشرين، فحتى عام 1900 كان من الممكن جمع العلوم المعرفية جميعها في 80 كتاب، أما الآن فلا يمكن جمع العلوم المعرفية في أقل من 100 ألف كتاب. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
العدد الأولي هو ذلك العدد الذي لا يقبل القسمة إلا نفسه والواحد الصحيح . .
وأقل الأعداد الأولية هي: 2 ، 3 ، 5 ، 7 ، 11 ، 13 ، 17 ، 19 ، 23 ، 29 ، 31 ، 37 . . . .
وجميع الأعداد الأولية أعداد فردية باستثناء (2).
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
أوّل من استخدم الجذر التربيعي هو عالم الرياضيات المسلم محمد بن موسى الخوارزمي، وأوّل من استعمله للأغراض الحسابية هو العالم أبو الحسن علي بن محمد القلصادي الأندلسي، الذي ولد عام 825 هجرية وتوفي سنة 891 هجرية، وانتشر هذا الرمز في مختلف لغات العالم.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| الأرقام التي نستعملها اليوم في كتابة الأعداد العربية:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
الأرقام المتناهية في الصغر:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
استخدم النظام الدولي للوحدات بعض الرموز والألفاظ الإغريقية للتعبير عن مضاعفات الأعداد الكبيرة، وكذا كسورها، وبالتالي أمكن التعبير عن أكبر وأصغر الأعداد كما يلي:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
وهناك أعداد كبيرة جدًا لا نستخدمها في حياتنا اليومية بصورة كبيرة ، ويستخدمها بعض العلماء والباحثين، كالفلكيين الذين يتعاملون مع الأعداد الضخمة جداً. ومن هذه الأعداد:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
نماذج من عجائب الأرقام: |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| عجائب الرقم واحد: 1 × 1 = 1 11 × 11 = 121 111 × 111 = 12321 1111 × 1111 = 1234321 11111 × 11111 = 123454321 111111 × 111111 = 12345654321 1111111 × 1111111 = 1234567654321 11111111 × 11111111 = 123456787654321 111111111 × 111111111 = 12345678987654321 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| الرقم ثلاثة: اضرب 37 × الرقم 3 ومضاعفاته: 37 × 3 = 111 37 × 6 = 222 37 × 9 = 333 37 × 12 = 444 37 × 15 = 555 37 × 18 = 666 37 × 21 = 777 37 × 24 = 888 37 × 27 = 999 37 × 30 = 1110 37 × 33 = 1221 37 × 36 = 1332 وهكذا ….. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| الرقم ثلاثة: اضرب 37 × الرقم 3 ومضاعفاته (صيغة أخرى): 1 × 3 × 37 = 111 2 × 3 × 37 = 222 3 × 3 × 37 = 333 4 × 3 × 37 = 444 5 × 3 × 37 = 555 6 × 3 × 37 = 666 7 × 3 × 37 = 777 8 × 3 × 37 = 888 9 × 3 × 37 = 999 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| الرقم ثلاثة أيضا: اضرب 12345679 × الرقم 3 ومضاعفاته: 12345679 × 3 = 37037037 12345679 × 6 =74074074 12345679 × 9 = 111111111 12345679 × 12 = 148148148 12345679 × 15 = 185185185 12345679 × 18 = 222222222 12345679 × 21 = 259259259 12345679 × 24 = 296296296 12345679 × 27 = 333333333 12345679 × 30 = 370370370 12345679 × 33 = 407407407 12345679 × 36 = 444444444 12345679 × 39 = 481481481 12345679 × 42 = 518518518 12345679 × 45 = 555555555 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| الرقمين: خمسة وثمانية: 5 × 8 = 40 5 × 88 = 440 5 × 888 = 4440 5 × 8888 = 44440 5 × 88888 = 444440 وهكذا….. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
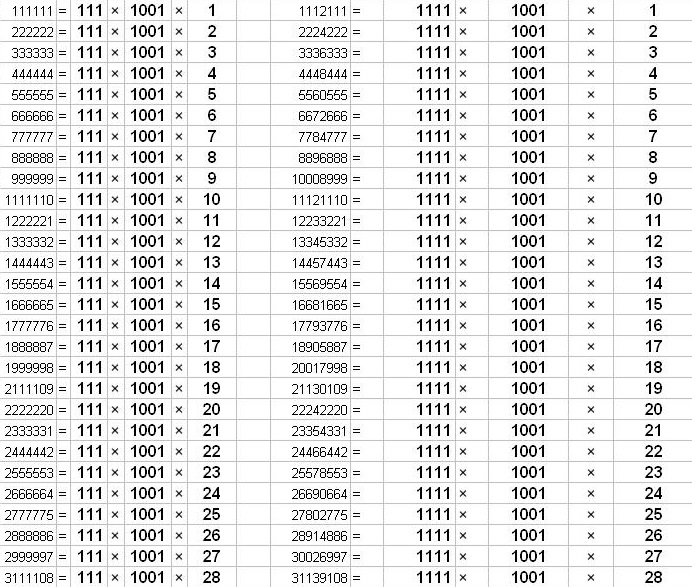
| عجائب الرقم سبعة: إذا ضربنا الرقم 7 ومضاعفاته في العدد 15873 فستنتج ستة أرقام مكررة: 7×15873=111111 14×15873=222222 21×15873=333333 28×15873=444444 35×15873=555555 42×15873 = 666666 49×15873 = 777777 56×15873 = 888888 63×15873 = 999999 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| الرقم 7 بصيغة أخرى: 1×7×15873=111111 2×7×15873=222222 3×7×15873=333333 4×7×15873=444444 5×7×15873=555555 6×7×15873=666666 7×7×15873=777777 8×7×15873=888888 9×7×15873=999999 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| عجائب الرقم ثمانية: 1×8+1=9 12×8+2=98 123×8+3=987 1234×8+4=9876 12345×8+5=98765 123456×8+6=987654 1234567×8+7=9876543 12345678×8+8=98765432 123456789×8+9= 987654321 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ومن عجائب الرقم ثمانية أيضا:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| من عجائب الرقم تسعة: 9 × 1 = 9 9 × 2 = 18 9 × 3 = 27 9 × 4 = 36 9 × 5 = 45 9 × 6 = 54 9 × 7 = 63 9 × 8 = 72 9 × 9 = 81 9 × 10 = 90 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| وأيضا من عجائب الرقم تسعة:
1 × 9 = 9 12 × 9 = 108 123 × 9 = 1107 1234 × 9 = 11106 12345 × 9 = 11105 123456 × 9 = 1111104 1234567 × 9 = 11111103 12345678 × 9 = 111111102 123456789 × 9 = 1111111101 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ومن عجائب الرقم تسعة أيضا: 1 × 9 + 2 = 11 12 × 9 + 3 = 111 123 × 9 + 4 = 1111 1234 × 9 + 5 = 11111 12345 × 9 + 6 = 111111 123456 × 9 + 7 = 1111111 1234567 × 9 + 8 = 11111111 12345678 × 9 + 9 = 111111111 123456789 × 9 + 10 = 1111111111 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| وعن الرقم تسعة كذلك: 1 × 9 = 9 × 12345679 = 111111111 2 × 9 = 18 × 12345679 = 222222222 3 × 9 = 27 × 12345679 = 333333333 4 × 9 = 36 × 12345679 = 444444444 5 × 9 = 45 × 12345679 = 555555555 6 × 9 = 54 × 12345679 = 666666666 7 × 9 = 63 × 12345679 = 777777777 8 × 9 = 73 × 12345679 = 888888888 9 × 9 = 81 × 12345679 = 999999999 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| من عجائب الرقم تسعة كذلك: 0×9+8=8 9×9+7=88 98×9+6=888 987×9+5=8888 9876×9+4=88888 98765×9+3=888888 4 98765×9+2=8888888 9876543×9+1=88888888 98765432×9+0=888888888 وأخرى: 987654321 × 9 = 8888888889 98765432 × 9 = 888888888 9876543 × 9 = 88888887 987654 × 9 = 8888886 98765 × 9 = 888885 9876 × 9 = 88884 987 × 9 = 8883 98 × 9 = 882 9 × 9 = 81 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| الرقم تسعة وتسعين: 99 × 1 = 99 99 × 2 = 198 99 × 3 = 297 99 × 4 = 396 99 × 5 = 495 99 × 6 = 594 99 × 7 = 693 99 × 8 = 792 99 × 9 = 891 99 × 10 = 990 لاحظ: الرقم الأوسط دائماً في ناتج الضرب = 9 مجموع الرقمين الأول والثالث دائماً = 9 ينقص رقم الآحاد كل مرة بمقدار 1 بينما يزداد رقم العشرات بمقدار 1 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| خواص الأعداد: العدد 1 هو أصل العدد ومنشأه وهو يعد العدد كله ، الأزواج والأفراد جميعاً. العدد 2 هو أول العدد مطلقاً وهو يعد نصف العدد الأزواج دون الأفراد . العدد 3 هو أول عدد الأفراد وهو يعد ثلث الأعداد وتارة الأفراد وتارة الأزواج . العدد 4 هو أول عدد مجذور – أي تربيع . العدد 5 هو أول عدد دائري ويقال كروي . العدد 6 هو أول عدد تام . العدد 7 هو أول عدد كامل . العدد 8 هو أول عدد مكعب . العدد 9 هو أول عدد فرد مجذور – وإنه آخر مرتبة الآحاد . العدد 10 هو أول مرتبة العشرات . العدد 11 هو أول عدد أصم . العدد 12 هو أول عدد زائد . |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| اضرب عمرك × 13837 × 73 = ….وشاهد النتيجة… سوف تدهشك | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| العدد 3025: – – قَسِمهُ إلى جُزأين : 25 ، 30 – – أوجد مجموع الجزأين : 25 + 30 = 55 اضرب الناتج في نفسه : 55 × 55 = 3025 – – نلاحظ أن الناتج هو العدد الأصلي |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| أخيرا تأمل هذا:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||